День программиста или маленькая программка на asm’е.
Старый добрый debug.exe, с легкой подачи Di, позволил написать праздничный вариант программы "Hello, world!"
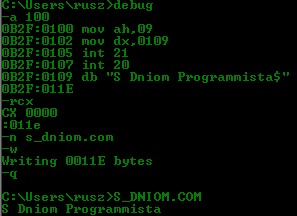
-a 100
0B2F:0100 mov ah,09
0B2F:0102 mov dx,0109
0B2F:0105 int 21
0B2F:0107 int 20
0B2F:0109 db "S Dniom Programmista$"
0B2F:011E
-rcx
CX 0000
:011e
-n s_dniom.com
-w
Writing 0011E bytes
-q
Объектно-ориентированное программирование. Введение.
Существует два основных способа проектирования программных систем – структурное проектирование, основанное на алгоритмической декомпозиции, и объектно-ориентированное проектирование, основанное на объектно-ориентированной декомпозиции. Разделение по алгоритмам концентрирует внимание на порядке происходящих событий, а разделение по объектам придает особое значение агентам, которые являются либо объектами, либо субъектами действия. Однако эти способы, по сути, ортогональны, поэтому нельзя сконструировать сложную систему одновременно двумя способами. Необходимо начать разделение системы либо по алгоритмам, либо по объектам, а затем, используя полученную структуру, попытаться рассмотреть проблему с другой точки зрения.
Алгоритмическую декомпозицию можно представить как обычное разделение алгоритмов, где каждый модуль системы выполняет один из этапов общего процесса. При объектно-ориентированной декомпозиции каждый объект обладает своим собственным поведением, и каждый из них моделирует некоторый объект реального мира. С этой точки зрения объект является вполне осязаемой вещью, которая демонстрирует вполне определенное поведение. Объекты что-то делают, и мы можем, послав им сообщение, попросить их выполнить некоторые операции.
Объектная декомпозиция имеет несколько преимуществ перед алгоритмической:
• объектная декомпозиция уменьшает размер программных систем за счет повторного использования общих механизмов, что приводит к существенной экономии выразительных средств;
• объектно-ориентированные системы более гибки и проще эволюционируют со временем, потому что их схемы базируется на устойчивых промежуточных формах. Действительно, объектная декомпозиция существенно снижает риск при создании сложной программной системы, так как она развивается из меньших систем, в которых мы уже уверены;
• объектная декомпозиция помогает нам разобраться в сложной программной системе, предлагая нам разумные решения относительно выбора подпространства большого пространства состояний.
В объектно-ориентированном анализе существует четыре основных типа моделей: динамическая, статическая, логическая и физическая. Через них можно выразить результаты анализа и проектирования, выполненные в рамках любого проекта. Эти модели в совокупности семантически достаточно богаты и универсальны, чтобы разработчик мог выразить все заслуживающие внимания стратегические и тактические решения, которые он должен принять при анализе системы и формировании ее архитектуры. Кроме того, эти модели достаточно полны, чтобы служить техническим проектом реализации практически на любом объектно-ориентированном языке программирования.
Фактически все сложные системы можно представить одной и той же (канонической) формой – в виде двух ортогональных иерархий одной системы: классов и объектов. Каждая иерархия является многоуровневой, причем в ней классы и объекты более высокого уровня построены из более простых. Какой класс или объект выбран в качестве элементарного, зависит от рассматриваемой задачи. Объекты одного уровня имеют четко выраженные связи, особенно это касается компонентов структуры объектов. Внутри любого рассматриваемого уровня находится следующий уровень сложности. Структуры классов и объектов не являются независимыми: каждый элемент структуры объектов представляет специфический экземпляр определенного класса. Объектов в сложной системе обычно гораздо больше, чем классов. С введением структуры классов в ней размещаются общие свойства экземпляров классов.
Структурный подход состоит в декомпозиции (разбиении) системы на элементарные функции, т.е., система разбивается на функциональные подсистемы, которые в свою очередь делятся на подфункции, подразделяемые на задачи и так далее. Процесс разбиения продолжается вплоть до конкретных процедур. При этом создаваемая система сохраняет целостное представление, в котором все составляющие компоненты взаимоувязаны.
Все наиболее распространенные методологии структурного подхода базируются на ряде общих принципов. В качестве двух базовых принципов используются следующие:
• принцип решения сложных проблем путем их разбиения на множество меньших независимых задач, легких для понимания и решения;
• принцип организации составных частей проблемы в иерархические древовидные структуры с добавлением новых деталей на каждом уровне – так называемый принцип иерархического упорядочивания.
В структурном анализе используются в основном две группы средств, иллюстрирующих функции, выполняемые системой и отношения между данными. Каждой группе средств соответствуют определенные виды моделей (диаграмм), наиболее распространенными среди которых являются следующие:
• SADT (Structured Analysis and Design Technique) модели и соответствующие функциональные диаграммы;
• DFD (Data Flow Diagrams) диаграммы потоков данных;
• ERD (Entity-Relationship Diagrams) диаграммы "сущность-связь".
На стадии проектирования системы модели расширяются, уточняются и дополняются диаграммами, отражающими ее структуру.
Перечисленные модели в совокупности дают полное описание системы независимо от того, является ли она существующей или вновь разрабатываемой. Состав диаграмм в каждом конкретном случае зависит от необходимой полноты описания системы.
Сортировка выбором (выделением)
В данной сортировке сначала ищется (выбирается) минимальный элемент в массиве и меняется местами с первым элементом. Первый элемент из дальнейшей сортировки выбывает.
void selection_sort(int *mArray, int _size)
{
for(int i = 0; i < _size; i++)
{
int k = i;
for(int j = k + 1; j < _size; j++)
{
if(mArray[k] > mArray[j]) k = j;
}
if(i != k) std::swap(mArray[i], mArray[k]);
}
}
Сортировка "Шейкер"
int shaker_sort(int *&mArray, int _size)
{
int L = 0;
int R = _size - 1;
int k = _size - 1;
do
{
for( int j = R; j >= L; j--) //Ставим на место самый маленький элемент
{
if(mArray[j-1] > mArray[j])
{
std::swap(mArray[j], mArray[j-1]);
k = j;
}
}
L = k + 1; //Сдвигаем левую границу
for(int j = L; j <= R; j++) //Ставим на место самый большой элемент
{
if(mArray[j-1] > mArray[j])
{
std::swap(mArray[j], mArray[j-1]);
k = j;
}
}
R = k - 1; //Сдвигаем правую границу
} while(L < R);
}
Последовательный (линейный) поиск
Поиск последовательно проверяет все элементы, а так же достижение конца массива.
int line_seach(int *mArray, int _size, int find_el)
{
int position = 0;
for(;(mArray[position] != find_el) && (position < _size); position++); //Поиск
position++; //Корректируем номер позиции
return position <= _size ? position : 0; //Если элемент найден, то возвращаем его позицию, если нет, то 0
}
Двоичный поиск (только для отсортированных массивов)
Массив делится пополам и граница сдвигается в соответствии с тем, где, возможно, находится искомый элемент.
Боевой пример:
int dv_seach(int *mArray, int _size, int find_el)
{
int left = 0, right = _size - 1, m; //Устанавливаем границы
while(left < right)
{
m = (left + right) / 2; //Выбираем середину
if (find_el > mArray[m]) left = m + 1; //Если элемент в середине рассматриваемого
//участка больше искомого, то сдвигаем границу влево
else right = m; //Если меньше - вправо
}
return find_el == mArray[left] ? left + 1 : 0; //Если элемент найден, то возвращаем его позицию, если нет, то 0
}
Планы
Итак, в планах написать и оформить:
Алгоритмы поиска символа:
1. Последовательный (линейный) поиск (уже есть)
2. Поиск с барьером (уже есть)
3. Двоичный поиск (бинарный, деление пополам) - только для отсортированных массивов (уже есть)
Алгоритмы поиска слова:
1. Прямой поиск (уже есть)
2. КМП поиск (уже есть) дооформить
3. Алгоритм Бойера-Мура (уже есть (упрощенный(?)))
Алгоритмы сортировки:
1. Сортировка обменом (метод «пузырька) (C++ и Java) дооформить
2. Сортировка «Шейкер» (уже есть) дооформить
3. Сортировка вставками (включением) (уже есть) дооформить
4. Сортировка выбором (выделением) (уже есть)
5. Алгоритм Шелла (уже есть)
6. Алгоритм Хоара (быстрая сортировка) (C++, Pascal)
7. Пирамидальная сортировка (уже есть)
8. Гномья сортировка (Gnome Sort) (Java)
Динамические структуры данных:
1. Линейный односвязный список
2. Очередь
3. Стек
4. Дек
5. Кольцевой односвязный список
6. Линейный двусвязный список
7. Бинарное дерево
7.1. AVL дерево
7.2. Красно-черное дерево
Алгоритмы сжатия информации:
1. Алгоритм Шеннона и Фако
2. Алгоритм Хафмана
3. Алгоритм скошенного дерева
Поиск с барьером
Алгоритм поиска заключается в установке "барьера" - искомого элемента - в конец массива.
Таким образом пропадает необходимость проверки на достижение конца массива.
Боевой пример:
int barrier_seach(int *mArray, int _size, int find_el)
{
int position = 0;
if (mArray[_size-1] != find_el) //Проверим, нет ли искомого элемента на последней позиции
{
mArray[_size-1] = find_el; //Установим "барьер"
for(;mArray[position] != find_el; position++); //Поиск
position++; //Корректируем номер позиции
}
else return _size; //Если искомый элемент на последней позиции, то возвращаем размер
return position < _size ? position : 0; //Если элемент найден, то возвращаем его позицию, если нет, то 0
}
Сортировка обменом (метод "пузырька")
void buble_sort(int mArray[], int mArr_size)
{
for(int i = 1; i < mArr_size; i++)
for (int k = i; (k >= 1) && (mArray[k] < mArray[k-1]); k--)
std::swap(mArray[k],mArray[k-1]);
}
Сортировка вставками (включением)
void insertSort(int a[], int size)
{
int x, i, j;
for (i = 1; i < size; i++) // цикл проходов, i - номер прохода
{
x = a[i]; // сохраняем элемент, место которому необходимо найти
for (j = i; j > 0 && a[j-1] > x; j--) // поиск места элемента в готовой последовательности
a[j] = a[j-1]; // сдвигаем элемент направо, пока не дошли
a[j] = x; // место найдено, вставить элемент
}
}